
(HPO only) Be familiar with and able to prove basic theorems and solve problems in the area of Iterated Function Systems and fractal (Hausdorff, Minkowski) dimensions.
#FRACTAL GEOMETRY HOW TO#
Understand how to use fractal geometry to model rough data and natural shapes.Ĥ. Be able to analyse 1-D dynamical systems in terms of attractors, basins and cascades of bifurcations.ģ. Be able to construct and analyse a wide range of fractals.Ģ. Upon successful completion of this course, students will The cosmic web structure is studied with the concepts and methods of fractal geometry, employing the adhesion model of cosmological dynamics as a basic. Upon successful completion, students will have the knowledge and skills to: In computer laboratory sessions students learn how the mathematical results can be applied in practice by running and modifying simple Python programs. However, all students are invited to sit in on the HPO special lectures which provide the rigorous mathematical foundations. It is a geometrical object comprised of infinitely many worlds.

The complexity of natures shapes differs in kind, not merely degree, from that of the shapes of ordinary geometry, the geometry of fractal shapes. Clouds are not spheres, mountains are not cones, and lightening does not travel in a straight line. For our purposes, therein lies our definition of a fractal. 15.79 98 Used from 9.59 11 New from 78.95 1 Collectible from 244.73. The key definitions and theorems are stated but few proofs of theorems are given. To put simply, we can never reach the fundamental components of a figure that is a fractal we can only observe smaller and smaller worlds (patterns in the figure that continue for infinity). The key ideas are introduced in an intuitive way. Fractals, the crux of fractal geometry, are infinitely complex & detailed patterns that are self-similar across different scales theyre mathematical objects. They can be called fathers of this area, working around the year 1900. It is new and rapidly developing.1 Fractal geometry itself goes back to Caratheodory, Hausdor, and Besicovich. These areas intersect, and this is what we are interested in.

Relationships between fractal geometry and discrete dynamical systems and chaotic dynamics are emphasized, including symbolic dynamics, stability of attractors, bifurcations and routes to chaos. This course is about fractal geometry and dynamical systems. Fractals surround us in so many different aspects of life.
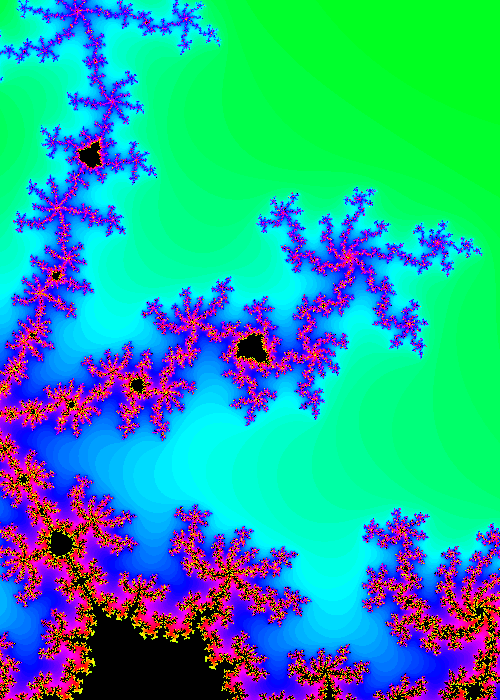
In essence, a Fractal is a pattern that repeats forever, and every part of the Fractal, regardless of how zoomed in, or zoomed out you are, it looks very similar to the whole image. Basic topological and geometrical language to describe and model rough, ("fractal") objects is developed. Editorial note: This letter seems to be a response to a journal article by Kenneth Hsu and Andreas Hsu entitled Fractal geometry of music and published. A Fractal is a type of mathematical shape that are infinitely complex. Addeddate 01:30:58 Identifier FractalGeometry Identifier-ark ark:/13960/t4mk7c24c Ocr ABBYY FineReader 8.0 Ppi 300. This course introduces basic mathematical techniques of fractal geometry and dynamical systems, aimed towards understanding and modeling natural shapes and forms from leaves to coastlines. Topics Mathematics Collection opensource Language English.


 0 kommentar(er)
0 kommentar(er)
